> この記事では、MSM アルゴリズム、楕円曲線点加算アルゴリズム、モンゴメリ乗算アルゴリズムなどを詳細に分析し、BLS12\_381 曲線点加算における GPU と FPGA の性能差を比較します。**作者: スター・リー**プライバシー証明、計算証明、コンセンサス証明など、ゼロ知識証明技術はますます広く使用されています。より優れたアプリケーション シナリオを模索するうちに、多くの人が徐々に、ゼロ知識証明によってパフォーマンスがボトルネックになっていることが判明しました。 Trapdoor Tech チームは、2019 年からゼロ知識証明テクノロジーを深く研究し、効率的なゼロ知識証明アクセラレーション ソリューションを模索してきました。 GPU または FPGA は、現在市場で比較的一般的なアクセラレーション プラットフォームです。この記事では、MSM の計算から始めて、FPGA と GPU で高速化されたゼロ知識証明計算の長所と短所を分析します。##TL;DRZKP は将来性の高い技術です。ゼロ知識証明テクノロジーを採用するアプリケーションがますます増えています。ただし、ZKP アルゴリズムは多数あり、さまざまなプロジェクトで異なる ZKP アルゴリズムが使用されています。同時に、ZKP 証明の計算パフォーマンスは比較的劣ります。本稿では、MSMアルゴリズム、楕円曲線点加算アルゴリズム、モンゴメリ乗算アルゴリズムなどを詳細に分析し、BLS12\_381曲線点加算におけるGPUとFPGAの性能差を比較します。一般に、ZKP 証明コンピューティングの観点からは、短期 GPU には、高スループット、高コストパフォーマンス、プログラマビリティなどの明らかな利点があります。相対的に言えば、FPGA には消費電力の点で一定の利点があります。長期的には、ZKP 計算に適した FPGA チップ、または ZKP 用にカスタマイズされた ASIC チップが登場する可能性があります。## ZKP アルゴリズム複合体ZKPとは、Zero Knowledge Proof技術(Zero Knowledge Proof)の総称です。主に zk-SNARK と zk-STARK の 2 つの分類があります。 zk-SNARK の現在の一般的なアルゴリズムは、Groth16、PLONK、PLOOKUP、Marlin、Halo/Halo2 です。 zk-SNARK アルゴリズムの反復は主に 2 つの方向に沿って行われます: 1/信頼できるセットアップが必要かどうか 2/回路構造のパフォーマンス。 zk-STARK アルゴリズムの利点は、信頼できるセットアップが必要ないにもかかわらず、検証計算の量が対数線形であることです。zk-SNARK/zk-STARK アルゴリズムのアプリケーションに関する限り、さまざまなプロジェクトで使用されるゼロ知識証明アルゴリズムは比較的分散しています。 zk-SNARK アルゴリズムのアプリケーションでは、PLONK/Halo2 アルゴリズムはユニバーサルであるため (信頼できるセットアップは必要ありません)、アプリケーションはますます増える可能性があります。## PLONK は計算量を証明しますPLONK アルゴリズムを例として、PLONK 証明の計算量を分析します。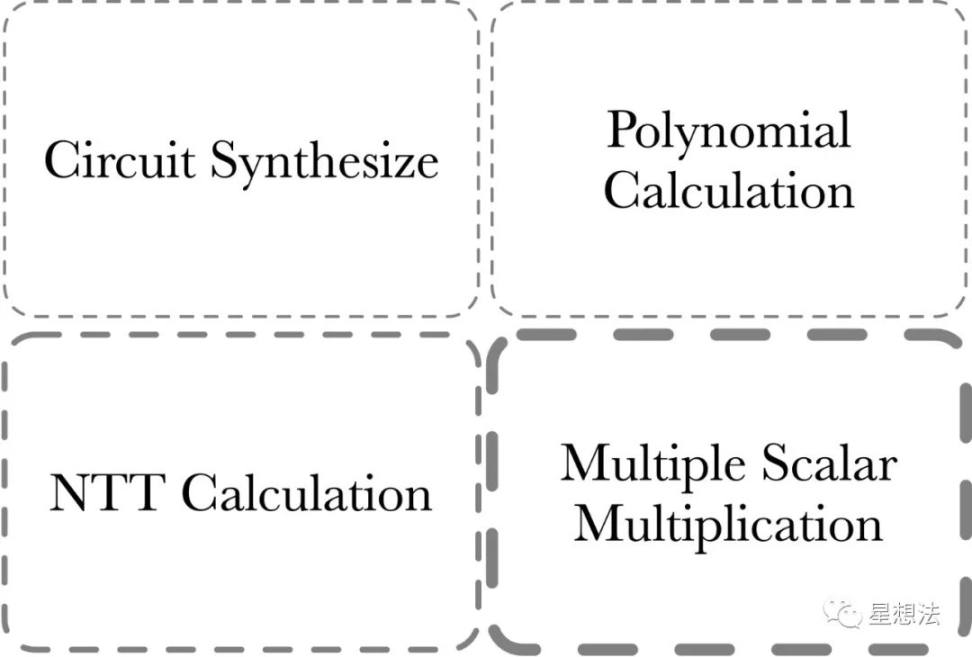PLONK 証明部分の計算量は 4 つの部分で構成されます。1/ MSM - 複数のスカラー乗算。 MSM は、多項式コミットメントを計算するためによく使用されます。2/ NTT Computation - ポイント値と係数表現の間の多項式変換。3/ 多項式の計算 - 多項式の加算、減算、乗算、除算。多項式評価 (uation) など。4/ 回路合成 - 回路合成。この部分の計算は回路の規模/複雑さに関係します。一般的に、回路合成部分の計算量は判定やループロジックが多く、並列度は比較的低いため、CPU による計算に適しています。一般に、ゼロ知識証明の高速化とは、最初の 3 つの部分の計算高速化を指します。このうち、比較的計算量が多いのは MSM で、次に NTT が続く。## MSM とはMSM (Multiple Scalar Multiplication) は、楕円曲線上の与えられた一連の点とスカラーを参照し、これらの点を加算した結果に対応する点を計算します。たとえば、楕円曲線上の一連の点が与えられたとします。指定された 1 つの曲線からの楕円曲線点の固定セットを指定すると、次のようになります。[G\_1、G\_2、G\_3、...、G\_n]ランダム係数:および指定されたスカラー場からランダムにサンプリングされた有限体の要素:[s\_1、s\_2、s\_3、...、s\_n]MSM は、楕円曲線点 Q を取得するための計算です。Q = \sum\_{i=1}^{n}s\_i\*G\_i業界では一般に、MSM 計算を最適化するためにピッペンジャー アルゴリズムを採用しています。ピッペンジャーのアルゴリズムのプロセスの概略図を詳しく見てみましょう。ピッペンジャー アルゴリズムの計算プロセスは 2 つのステップに分かれています。1/ スカラーは Windows に分割されます。スカラーが 256 ビット、ウィンドウが 8 ビットの場合、すべてのスカラーは 256/8=32 のウィンドウに分割されます。 Window の各層は「バケット」を使用して中間結果を一時的に保存します。 GW\_x は、1 つのレイヤー上の累積結果のポイントです。 GW\_x の計算も比較的簡単で、層内の各スカラーを順番に走査し、スカラー層の値をインデックスとして使用し、対応する G\_x を対応するバケットに追加します。実際、原理は比較的単純で、2 点の加算係数が同じ場合、スカラーを加算する前に 2 点を 2 回加算するのではなく、最初に 2 点を加算してからスカラーを再度加算します。2/ 各ウィンドウで計算されたポイントは二重加算によって累積され、最終結果が得られます。ピッペンジャーのアルゴリズムには、多くの変形最適化アルゴリズムもあります。いずれの場合も、MSM アルゴリズムの基礎となる計算は、楕円曲線上の点の追加です。異なる最適化アルゴリズムは、異なる追加ポイント数に対応します。## 楕円曲線点追加(Point Add)このサイトでは、「ショートワイエルシュトラス」形式の楕円曲線上の点加算のさまざまなアルゴリズムをご覧いただけます。2点の射影座標をそれぞれ(x1, y1, z1)、(x2, y2, z2)とすると、点加算結果(x3, y3, z3)は以下の計算式で計算できます。計算プロセスを詳細に説明する理由は、計算プロセス全体がほとんど整数演算であることを示すためです。整数のビット幅は、楕円曲線のパラメータによって異なります。いくつかの一般的な楕円曲線のビット幅を与えます。* BN256 - 256ビット* BLS12\_381 - 381 ビット* BLS12_377 - 377ビット* これらの整数演算はモジュロフィールド上の演算であることに特に注意してください。剰余加算/剰余減算は比較的単純であり、剰余乗算の原理と実装に焦点を当てます。## 模乘(モジュラー乗算)モジュロフィールドに対して 2 つの値 x と y を指定します。剰余乗算の計算は、x\*y mod p を参照します。これらの整数のビット幅が楕円曲線のビット幅であることに注意してください。剰余乗算の古典的なアルゴリズムは、モンゴメリ乗算 (MontgomeryMulplication) です。モンゴメリ乗算を実行する前に、被乗数をモンゴメリ表現に変換する必要があります。モンゴメリ乗算の計算式は次のとおりです。モンゴメリ乗算の実装アルゴリズムには、CIOS (Coarsely Integrated Operand Scanning)、FIOS (Finely Integrated Operand Scanning)、FIPS (Finely Integrated Product Scanning) などがあります。この記事では、さまざまなアルゴリズムの実装の詳細については詳しく紹介しません。興味のある読者はご自身で調査してください。FPGA と GPU のパフォーマンスの違いを比較するには、最も基本的なアルゴリズムの実装方法を選択します。簡単に言えば、剰余乗算アルゴリズムは、大数乗算と大数加算の 2 つの計算にさらに分割できます。 MSM の計算ロジックを理解した後、モジュラー乗算のパフォーマンス (スループット) を選択して、FPGA と GPU のパフォーマンスを比較できます。## 観察して考えるこのような FPGA 設計では、VU9P 全体が BLS12\_381 楕円曲線点でのスループットを提供できると推定できます。点加算 (add\_mix 方法) には、約 12 回のモジュラー乗算が必要です。 FPGAのシステムクロックは450Mです。同じモジュラー乗算/モジュラス加算アルゴリズムの下で、同じポイント加算アルゴリズムを使用すると、Nvidia 3090 のポイントとトラフプットの合計 (データ伝送率を考慮) は 500M/s を超えます。もちろん、計算全体にはさまざまなアルゴリズムが含まれており、FPGA に適したアルゴリズムもあれば、GPU に適したアルゴリズムもあります。同じアルゴリズム比較を使用する理由は、FPGA と GPU のコア コンピューティング能力を比較するためです。上記の結果に基づいて、ZKP プルーフ パフォーマンスの観点から GPU と FPGA の比較を要約します。## 要約するゼロ知識証明テクノロジーを採用するアプリケーションがますます増えています。ただし、ZKP アルゴリズムは多数あり、さまざまなプロジェクトで異なる ZKP アルゴリズムが使用されています。私たちの実践的なエンジニアリングの経験から、FPGA はオプションですが、現時点では GPU がコスト効率の高いオプションです。 FPGA は決定論的コンピューティングを好みます。これには、遅延と消費電力の利点があります。 GPU は高いプログラマビリティを備え、比較的成熟したハイパフォーマンス コンピューティング フレームワークを備え、開発反復サイクルが短く、スループット シナリオを好みます。
FPGA と GPU で高速化されたゼロ知識証明コンピューティングの長所と短所を理解するための記事
作者: スター・リー
プライバシー証明、計算証明、コンセンサス証明など、ゼロ知識証明技術はますます広く使用されています。より優れたアプリケーション シナリオを模索するうちに、多くの人が徐々に、ゼロ知識証明によってパフォーマンスがボトルネックになっていることが判明しました。 Trapdoor Tech チームは、2019 年からゼロ知識証明テクノロジーを深く研究し、効率的なゼロ知識証明アクセラレーション ソリューションを模索してきました。 GPU または FPGA は、現在市場で比較的一般的なアクセラレーション プラットフォームです。この記事では、MSM の計算から始めて、FPGA と GPU で高速化されたゼロ知識証明計算の長所と短所を分析します。
##TL;DR
ZKP は将来性の高い技術です。ゼロ知識証明テクノロジーを採用するアプリケーションがますます増えています。ただし、ZKP アルゴリズムは多数あり、さまざまなプロジェクトで異なる ZKP アルゴリズムが使用されています。同時に、ZKP 証明の計算パフォーマンスは比較的劣ります。本稿では、MSMアルゴリズム、楕円曲線点加算アルゴリズム、モンゴメリ乗算アルゴリズムなどを詳細に分析し、BLS12_381曲線点加算におけるGPUとFPGAの性能差を比較します。一般に、ZKP 証明コンピューティングの観点からは、短期 GPU には、高スループット、高コストパフォーマンス、プログラマビリティなどの明らかな利点があります。相対的に言えば、FPGA には消費電力の点で一定の利点があります。長期的には、ZKP 計算に適した FPGA チップ、または ZKP 用にカスタマイズされた ASIC チップが登場する可能性があります。
ZKP アルゴリズム複合体
ZKPとは、Zero Knowledge Proof技術(Zero Knowledge Proof)の総称です。主に zk-SNARK と zk-STARK の 2 つの分類があります。 zk-SNARK の現在の一般的なアルゴリズムは、Groth16、PLONK、PLOOKUP、Marlin、Halo/Halo2 です。 zk-SNARK アルゴリズムの反復は主に 2 つの方向に沿って行われます: 1/信頼できるセットアップが必要かどうか 2/回路構造のパフォーマンス。 zk-STARK アルゴリズムの利点は、信頼できるセットアップが必要ないにもかかわらず、検証計算の量が対数線形であることです。
zk-SNARK/zk-STARK アルゴリズムのアプリケーションに関する限り、さまざまなプロジェクトで使用されるゼロ知識証明アルゴリズムは比較的分散しています。 zk-SNARK アルゴリズムのアプリケーションでは、PLONK/Halo2 アルゴリズムはユニバーサルであるため (信頼できるセットアップは必要ありません)、アプリケーションはますます増える可能性があります。
PLONK は計算量を証明します
PLONK アルゴリズムを例として、PLONK 証明の計算量を分析します。
PLONK 証明部分の計算量は 4 つの部分で構成されます。
1/ MSM - 複数のスカラー乗算。 MSM は、多項式コミットメントを計算するためによく使用されます。
2/ NTT Computation - ポイント値と係数表現の間の多項式変換。
3/ 多項式の計算 - 多項式の加算、減算、乗算、除算。多項式評価 (uation) など。
4/ 回路合成 - 回路合成。この部分の計算は回路の規模/複雑さに関係します。
一般的に、回路合成部分の計算量は判定やループロジックが多く、並列度は比較的低いため、CPU による計算に適しています。一般に、ゼロ知識証明の高速化とは、最初の 3 つの部分の計算高速化を指します。このうち、比較的計算量が多いのは MSM で、次に NTT が続く。
MSM とは
MSM (Multiple Scalar Multiplication) は、楕円曲線上の与えられた一連の点とスカラーを参照し、これらの点を加算した結果に対応する点を計算します。
たとえば、楕円曲線上の一連の点が与えられたとします。
指定された 1 つの曲線からの楕円曲線点の固定セットを指定すると、次のようになります。
[G_1、G_2、G_3、...、G_n]
ランダム係数:
および指定されたスカラー場からランダムにサンプリングされた有限体の要素:
[s_1、s_2、s_3、...、s_n]
MSM は、楕円曲線点 Q を取得するための計算です。
Q = \sum_{i=1}^{n}s_i*G_i
業界では一般に、MSM 計算を最適化するためにピッペンジャー アルゴリズムを採用しています。ピッペンジャーのアルゴリズムのプロセスの概略図を詳しく見てみましょう。
ピッペンジャー アルゴリズムの計算プロセスは 2 つのステップに分かれています。
1/ スカラーは Windows に分割されます。スカラーが 256 ビット、ウィンドウが 8 ビットの場合、すべてのスカラーは 256/8=32 のウィンドウに分割されます。 Window の各層は「バケット」を使用して中間結果を一時的に保存します。 GW_x は、1 つのレイヤー上の累積結果のポイントです。 GW_x の計算も比較的簡単で、層内の各スカラーを順番に走査し、スカラー層の値をインデックスとして使用し、対応する G_x を対応するバケットに追加します。実際、原理は比較的単純で、2 点の加算係数が同じ場合、スカラーを加算する前に 2 点を 2 回加算するのではなく、最初に 2 点を加算してからスカラーを再度加算します。
2/ 各ウィンドウで計算されたポイントは二重加算によって累積され、最終結果が得られます。
ピッペンジャーのアルゴリズムには、多くの変形最適化アルゴリズムもあります。いずれの場合も、MSM アルゴリズムの基礎となる計算は、楕円曲線上の点の追加です。異なる最適化アルゴリズムは、異なる追加ポイント数に対応します。
楕円曲線点追加(Point Add)
このサイトでは、「ショートワイエルシュトラス」形式の楕円曲線上の点加算のさまざまなアルゴリズムをご覧いただけます。
2点の射影座標をそれぞれ(x1, y1, z1)、(x2, y2, z2)とすると、点加算結果(x3, y3, z3)は以下の計算式で計算できます。
計算プロセスを詳細に説明する理由は、計算プロセス全体がほとんど整数演算であることを示すためです。整数のビット幅は、楕円曲線のパラメータによって異なります。いくつかの一般的な楕円曲線のビット幅を与えます。
模乘(モジュラー乗算)
モジュロフィールドに対して 2 つの値 x と y を指定します。剰余乗算の計算は、x*y mod p を参照します。これらの整数のビット幅が楕円曲線のビット幅であることに注意してください。剰余乗算の古典的なアルゴリズムは、モンゴメリ乗算 (MontgomeryMulplication) です。モンゴメリ乗算を実行する前に、被乗数をモンゴメリ表現に変換する必要があります。
モンゴメリ乗算の計算式は次のとおりです。
モンゴメリ乗算の実装アルゴリズムには、CIOS (Coarsely Integrated Operand Scanning)、FIOS (Finely Integrated Operand Scanning)、FIPS (Finely Integrated Product Scanning) などがあります。この記事では、さまざまなアルゴリズムの実装の詳細については詳しく紹介しません。興味のある読者はご自身で調査してください。
FPGA と GPU のパフォーマンスの違いを比較するには、最も基本的なアルゴリズムの実装方法を選択します。
簡単に言えば、剰余乗算アルゴリズムは、大数乗算と大数加算の 2 つの計算にさらに分割できます。 MSM の計算ロジックを理解した後、モジュラー乗算のパフォーマンス (スループット) を選択して、FPGA と GPU のパフォーマンスを比較できます。
観察して考える
このような FPGA 設計では、VU9P 全体が BLS12_381 楕円曲線点でのスループットを提供できると推定できます。点加算 (add_mix 方法) には、約 12 回のモジュラー乗算が必要です。 FPGAのシステムクロックは450Mです。
同じモジュラー乗算/モジュラス加算アルゴリズムの下で、同じポイント加算アルゴリズムを使用すると、Nvidia 3090 のポイントとトラフプットの合計 (データ伝送率を考慮) は 500M/s を超えます。もちろん、計算全体にはさまざまなアルゴリズムが含まれており、FPGA に適したアルゴリズムもあれば、GPU に適したアルゴリズムもあります。同じアルゴリズム比較を使用する理由は、FPGA と GPU のコア コンピューティング能力を比較するためです。
上記の結果に基づいて、ZKP プルーフ パフォーマンスの観点から GPU と FPGA の比較を要約します。
要約する
ゼロ知識証明テクノロジーを採用するアプリケーションがますます増えています。ただし、ZKP アルゴリズムは多数あり、さまざまなプロジェクトで異なる ZKP アルゴリズムが使用されています。私たちの実践的なエンジニアリングの経験から、FPGA はオプションですが、現時点では GPU がコスト効率の高いオプションです。 FPGA は決定論的コンピューティングを好みます。これには、遅延と消費電力の利点があります。 GPU は高いプログラマビリティを備え、比較的成熟したハイパフォーマンス コンピューティング フレームワークを備え、開発反復サイクルが短く、スループット シナリオを好みます。